INTRODUCTION
Recently Ben
Brockert, a professional rocket engineer, suggested that I had
ignored an important issue in the design of small launch vehicles:
residual propellants. He was right and it is worth considering the
effects of residual propellants on small launch vehicle performance.
Residual propellants
are unutilized propellants. It is not possible (or sometimes
desirable) to burn 100% of the propellants. This restriction results
in unused propellants which do not contribute to propulsion, yet
whose mass remains with the rocket stage.
With solid rocket
engines, nearing the end of their burn duration, it is possible for
the chamber pressure to drop below a point where neither reasonable
combustion nor propulsion occurs. This can result in slivers of
unburned propellant which do not contribute to the thrust of the
vehicle in any meaningful way.
With liquid
propellant rocket engines, problems can also occur during the end of
the propellant feeding period. Conditions can arise where gases
instead of liquids are fed into the rocket engine or its pumping
systems. When the propellant in a tank gets low, effects like
sloshing can result in gases being ingested into the propellant feed
pipes instead of the propellants. Uneven mixture ratios can result in
a surplus of one propellant or the other. These situations can result
in catastrophic conditions which often must be avoided by the
designer.
To avoid the effects
of these conditions, rocket designers will often purposely design for
there to be residual propellants as part of the normal usage of the
rocket. In any case, the existence of residual propellants is almost
guaranteed. Their effect on the performance of launch vehicles must
be considered. They also effect the lower mass boundary for a useful
small launch vehicle.
RESIDUAL
PROPELLANTS IN THE ROCKET EQUATION
The rocket equation
can take the following form:
|

|
eqn(1)
|
Where:
 =
delta V or change in velocity
=
delta V or change in velocity
 = gravitational acceleration
= gravitational acceleration
 = specific impulse
= specific impulse
 =
=
 +
+
 +
+

 =
=
 +
+

 =
propellant mass
=
propellant mass
 = structural mass
= structural mass
 = payload mass
= payload mass
To account for
residual propellants, we need to break up the propellant mass into
two components:
 =
=
 +
+

 =
mass of utilized propellant
=
mass of utilized propellant
 =
mass of residual propellant
=
mass of residual propellant
We can express this
relationship by specifying a percentage term:
 =
Propellant Residual Percentage
=
Propellant Residual Percentage
and then the
representation of the propellant becomes:
 =
=
 +
+

 =
=

 =
=

Putting these terms
back into the rocket equation, we get:
|

|
Eqn(2)
|
We can see that the
residual propellant adds to the inert mass of the rocket and effects
its mass ratio. Additionally, only the utilized propellant effects
the actual delta V of the vehicle.
DESIGNING FOR
RESIDUAL PROPELLANTS
We often know a
delta V we wish the rocket stage to attain and we want to calculate
the masses of the various components which will produce that
performance given known, reasonable mass ratios that can be attained.
Therefore, we're interested in calculating the budget for the inert
mass and the amount of propellant for a desired performance and
payload.
Knowing that
residual propellants have an effect on the performance, we would like
to include that in the calculations. Therefore, we must rearrange the
rocket equation to consider these realities.
We can identify the
inert mass of the vehicle as a function of the propellant mass using
a parameter known as lambda:
 =
=

or
 =
=

For a nice
explanation of lambda, see:
[http://selenianboondocks.com/2010/02/rocket-equation-mod-1/].
Knowing the
"technology level" or structural sophistication of the
rocket design, we can pick characteristic values of lambda and apply
it to a newer design. Historical values of lambda for various launch
vehicles can be found at [
http://home.earthlink.net/~apendragn/atg/coef/ ].
We can represent the
entire rocket equation as a function of these new component ratios:
|

|
eqn(3)
|
Where:
 = delta V (velocity change)
= delta V (velocity change)
 = gravitational acceleration
= gravitational acceleration
 = specific impulse
= specific impulse
 = total propellant mass
= total propellant mass
 = Residual Propellant Percentage
= Residual Propellant Percentage
 = payload mass
= payload mass
 =
=

From this, we would
like to solve the equation to calculate the total propellant mass as
a function of the other components:

Then, given our Pr
and lambda ratios, we can calculate all other mass component values
from that results:
 =
=

 =
=

 =
=

If we let MR
be the mass ratio:

then we can simplify
our representation of the rocket equation





|

|
eqn(4)
|
The derivation of
the equation for calculating the total propellant mass, knowing the
other mathematical components is:











|

|
eqn(5)
|
We now have an
equation which calculates the total propellant mass as a function of
Ml, dV, g, Isp, Pr, and lambda.
REALISTIC
RESIDUAL PROPELLANT FRACTIONS
Exact figures on
realistic expectations for residual propellants are hard to obtain.
Ultimately it depends on your feed system design. However, Sutton [1]
suggests 0.5% to 2%. For the Saturn V S1C stage, residual values of
~1% LOX and ~1.7% RP1 were seen for an overall Pr of 1.3% [3].

But, a pump-fed
design with regenerative cooling in the combustion chamber will
reasonably have more residual propellants than a pressure-fed
ablative design. It all depends on the design and other factors.
However, it is not unrealistic to expect upwards of 2% residual
propellant in the initial design phase.
UNDERSTANDING THE
EFFECTS OF RESIDUAL PROPELLANTS ON ROCKET DESIGN
One thing we can do
to understand the effects of residual propellants on a rocket design
is to see the effects on one particular design.
Suppose we have a
stage which has a payload of 700 lbs which we want to have a delta V
of 7,500 feet per second (FPS) and which has an average Isp over
flight of 250 seconds. Suppose also that we have a lambda of 48%
(this is approximately the value of lambda for the Redstone missile).
We can look at the
results of designing the rocket with and without residual propellant
considerations.
Without
consideration of residual propellants (Pr = 0), using equations 4 and
5 we get:









Therefore, the
vehicle has the following specifications:




(GLOW = Gross
Lift Off Weight)
Now, let's presume
that we have 2% residual propellant left at the end of flight, but we
want a rocket that has the same performance capabilities:









Therefore, the same
performance vehicle with 2% Pr has the following specifications:




Two percent in
residual propellants required a vehicle which is about 22% heavier to
get the same performance as a vehicle which doesn't have any residual
propellants (e.g. utilizes 100% of its propellants).
Using the above
vehicle values as a baseline, we can graph the effects of residual
propellant versus the vehicle glow:

As can be seen, in
this example, the GLOW just about doubles between 0% and 5% residual
propellants for the same payload, lambda, delta V and Isp.
For a multistage
vehicle, these residual propellant effects compound, resulting in a
significantly larger overall vehicle.
If we consider a 3
stage vehicle, where each stage has the following specifications:
|
Stage 3
|
Payload
|
2.2 lbs
|
|
delta V
|
13750 fps
|
|
Isp
|
300 s
|
|
lambda
|
0.20
|
|
Stage 2
|
Payload
|
Stage 3
|
|
delta V
|
13750 fps
|
|
Isp
|
300 s
|
|
lambda
|
0.20
|
|
Stage 1
|
Payload
|
Stage 2
|
|
delta V
|
7500 fps
|
|
Isp
|
250
|
|
lambda
|
0.48
|
then we can compare
results for the GLOW. The results I get are:
|
|
Residual
Propellants Across the Stages
(units in
lbs)
|
|
STAGES
|
0%
|
1%
|
2%
|
5%
|
|
Stage 3
|
Ml
|
2.2
|
2.2
|
2.2
|
2.2
|
|
Mp
|
18.825
|
21.216
|
24.302
|
43.120
|
|
Ms
|
3.765
|
4.243
|
4.860
|
8.624
|
|
Mf
|
24.791
|
27.659
|
31.363
|
53.945
|
|
Stage 2
|
Ml
|
24.791
|
27.659
|
31.363
|
53.945
|
|
Mp
|
212.133
|
266.740
|
346.454
|
1075.325
|
|
Ms
|
42.427
|
53.348
|
69.291
|
211.465
|
|
Mf
|
279.351
|
347.747
|
447.107
|
1322.735
|
|
Stage 1
|
Ml
|
279.351
|
347.747
|
447.107
|
1322.735
|
|
Mp
|
1652.266
|
2279.107
|
3285.383
|
15270.945
|
|
Ms
|
793.088
|
1093.971
|
1576.984
|
7330.054
|
|
Mf
|
2724.704
|
3720.825
|
5309.475
|
23923.734
|
|
GLOW
|
2724.704
|
3720.825
|
5309.475
|
23923.734
|
|
Multiplier from 0% Pr
|
1X
|
1.37X
|
1.95X
|
8.78X
|
The design in the
first column is unrealistic whereas the designs in the other columns
are more realistic. It is unrealistic to expect 100% propellant
utilization and the effects of residual propellants can be
significant. Using a realistic value of 2% results in an almost
doubling of the vehicle GLOW over the design without residual
propellant considerations.
SUMMARY
This quick analysis
of the effects of residual propellants on the rocket equation and on
particular rocket designs suggests that residual propellants cannot
be ignored for practical rocket designs. The effects also illustrate
that realistic multistage rocket designs are likely double the
take-off mass to those of designs which do not consider residual
propellants.
REFERENCES
1. Sutton &
Biblarz, Rocket Propulsion Elements, Ninth Edition.
2. Selenian
Boondocks, A Simple Modification of the Rocket Equation [
http://selenianboondocks.com/2010/02/rocket-equation-mod-1/ ].
3. NASA, Saturn V
Flight Manual - SA 503, MSFC-MAN-503
[http://hdl.handle.net/2060/19750063889 ].




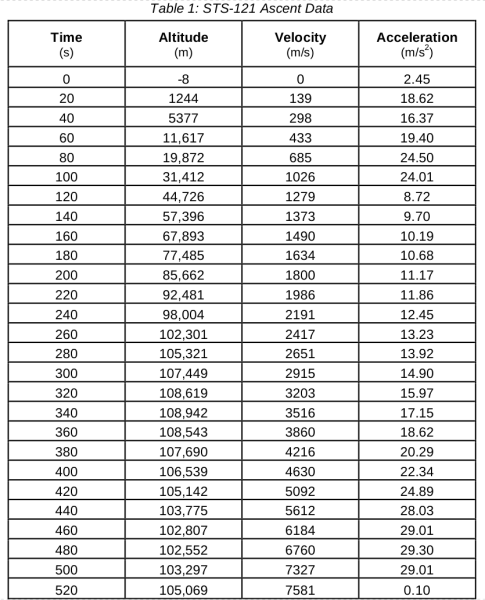
 ) and the velocity squared. Because of the velocity being squared, the dynamic pressure can increase significantly for small increases in velocity.
) and the velocity squared. Because of the velocity being squared, the dynamic pressure can increase significantly for small increases in velocity. Around 26 seconds, the dynamic pressure reaches a maximum of about 14 PSI (2016 PSF or 96.5 kPa). This is on top of the normal atmospheric pressure at the given altitude. When that pressure is applied over the frontal area of the vehicle, it can be a substantial force.
Around 26 seconds, the dynamic pressure reaches a maximum of about 14 PSI (2016 PSF or 96.5 kPa). This is on top of the normal atmospheric pressure at the given altitude. When that pressure is applied over the frontal area of the vehicle, it can be a substantial force.